Galileo, oddetallene, og elliptiske integral
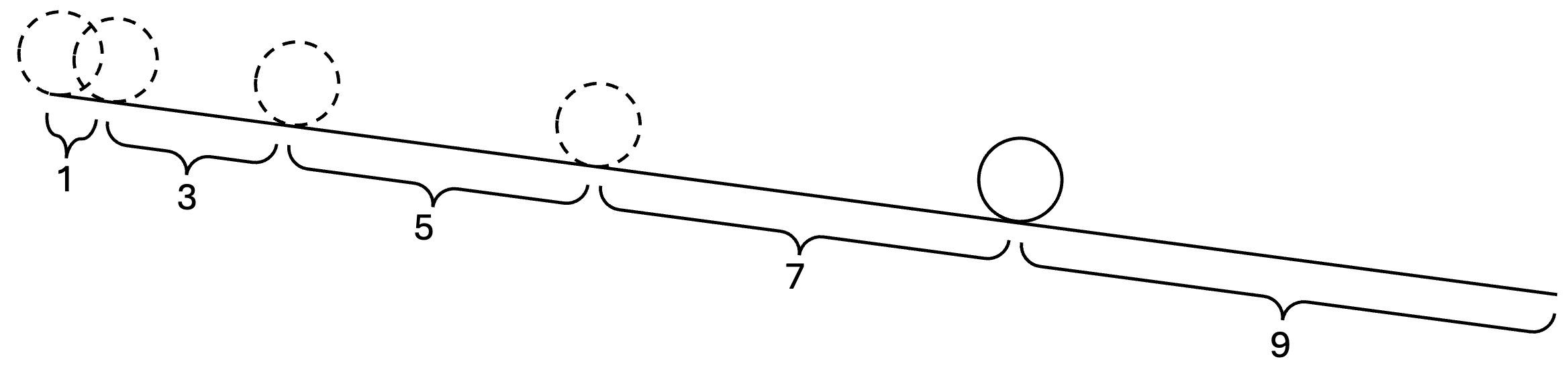
Galileo fant en merkelig sammenheng mellom oddetallene og akselerasjonen til rullende kuler
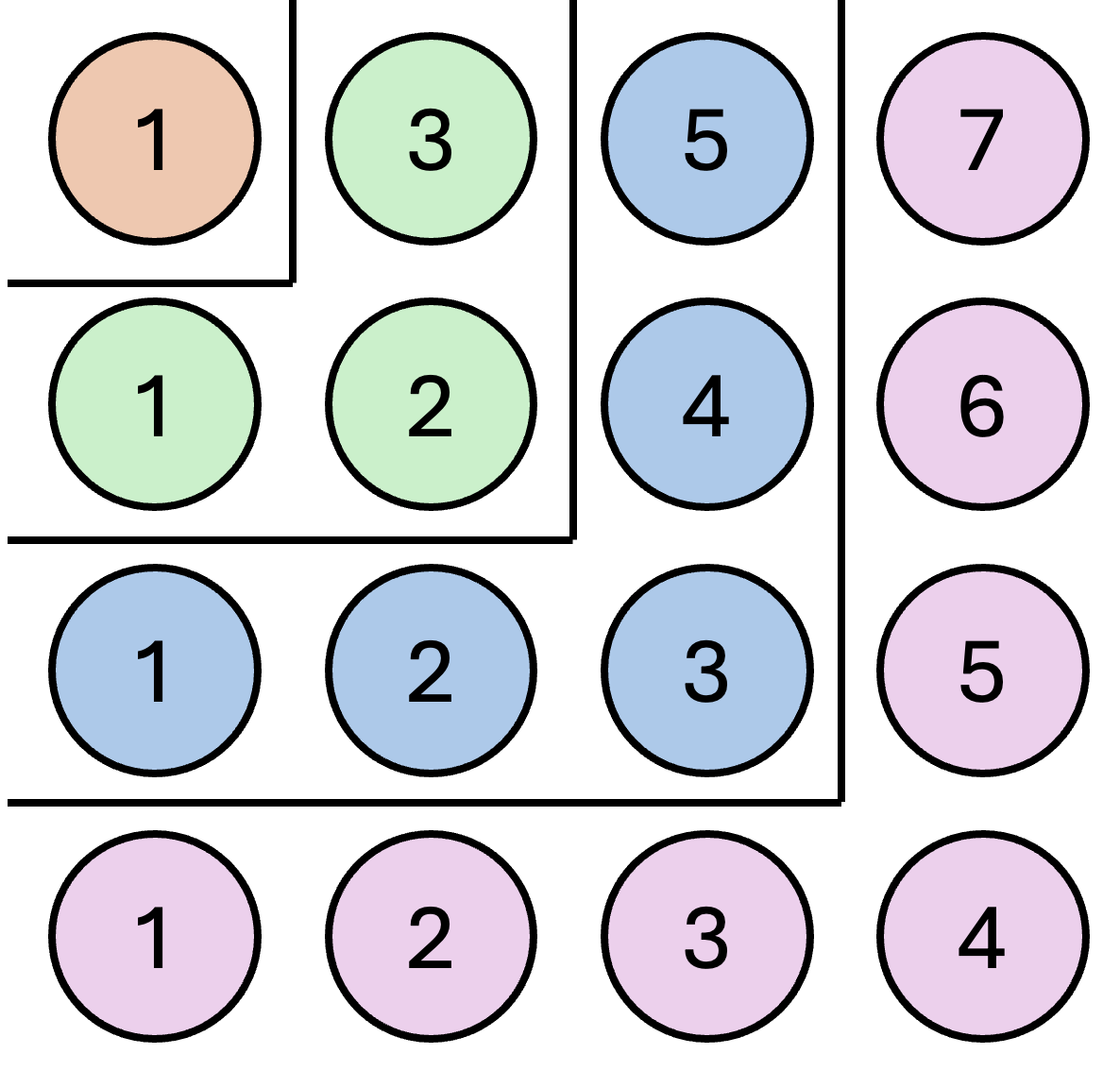
Alle tidsintervallene var et oddetall! (på formen $o=2n+1:n\in \mathbb{N}$ for de som liker notasjon) Det høres rart ut. Kan naturen telle? Og hvorfor valgte ikke gud heller de pene partallene? Selvfølgelig fordi den akkumulerte strekningen er proposjonal med $t^2$ som i $x(t) = at^2$. Eller summen av oddetallene er et kvadrat:
Galileo hadde ikke klokke, så han brukte først pulsen sin. Men den var så ustabil, så han begynte å bruke en pendel. Men pendelen måtte ha små utslag, for på store utslag, ble også den perioden ustabil.
Jeg ble nysgjerrig. Hva er perioden i de større utslagene? På skolen har vi alltid linearisert likningen for pendelen
\[l\ddot{\phi}+g\cos \phi=0\]med små vinkler, for da er $\sin \phi \approx \phi$.
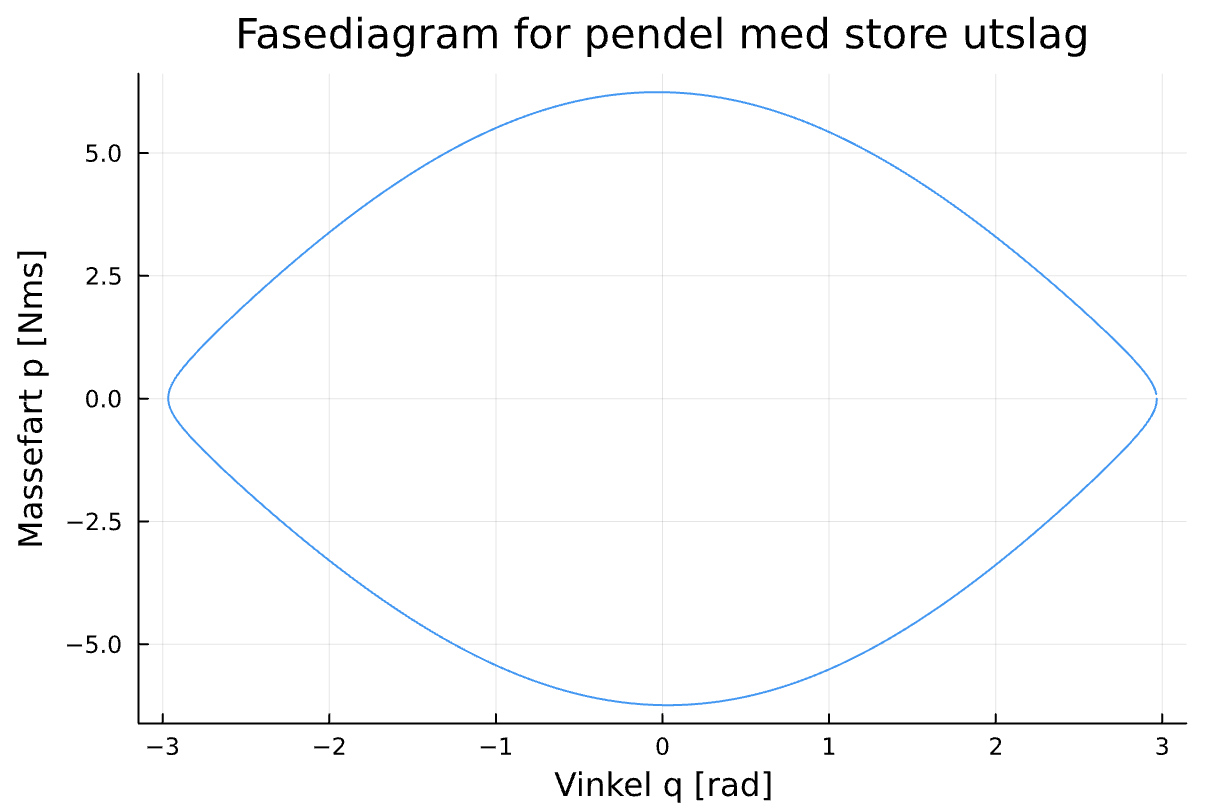
Men Galileo begynte jo med store vinkler. Jeg fikk en ide om å beregne perioden ved å integrere en runde i fasediagrammet. Beregne lengden til en strømlinje. Dette begynner å lukte av symplektisk geometri, som jeg har lyst til å lære mer om senere. Uansett. Likningene som beskriver strømlinjene er
\[\begin{align} \dot{p}&=-\frac{\partial H}{\partial q}\\ \dot{q}&=\frac{\partial H}{\partial p} \end{align}\]Hvor $H$ er total energi, og $p$ og $q$ er henholdsvis massefarten og posisjonen til systemet i faserommet. Heldigvis er dette et todimensjonalt system, så det blir lett å visualisere.
Energien er
\[H(p,q)=\frac{1}{2ml^{2}}p^{2}-mlg\cos q\]slik at strømlinjene kan beregnes med
\[\begin{align} \dot{p}&=-mlg\sin q\\ \dot{q}&=\frac{p}{ml^{2}} \end{align}\]Jeg kjørte dette i Julia og plottet en strømlinje:
Julia har noen pakker, feks DiffEqPhysics.jl, som gjør at man kan integrere hamiltonske systemer direkte, og benytte seg av den symplektiske geometrien til systemet for gunstigere energibevaring osv.
Her er den totale energien
function Pendulum_Hamiltonian(p, q, parameters, time)
m,l,g = parameters
1/(2m*l^2)*p^2 - m*l*g*cos(q)
end
Og så defineres problemet
prob = HamiltonianProblem(Pendulum_Hamiltonian, p0, q0, tspan, parameters)
Og integreres numerisk med en symplektisk integrator og med en callback som gjør at integratoren stopper etter en runde i fasediagrammet
solution = solve(prob, SymplecticEuler(), dt=0.01, callback=Callback_pendulum)
Det var mye trøbbel for å beregne perioden. I gamledager hadde de ikke Julia og heller ikke symplektiske integratorer, men de klarte å beregne perioden analytisk… med elliptiske integral! Hvorfor har vi ikke lært dette på skolen? Andrew Wiles brukte elliptiske kurver til å bevise fermats siste teorem, men jeg vet ikke om det er relatert.
\[\int_{0}^{2\pi}\frac{d\theta}{\sqrt{1-k^{2}\sin^{2}\theta}}\]